문제풀이 - 1512.Number of Good Pairs
문제
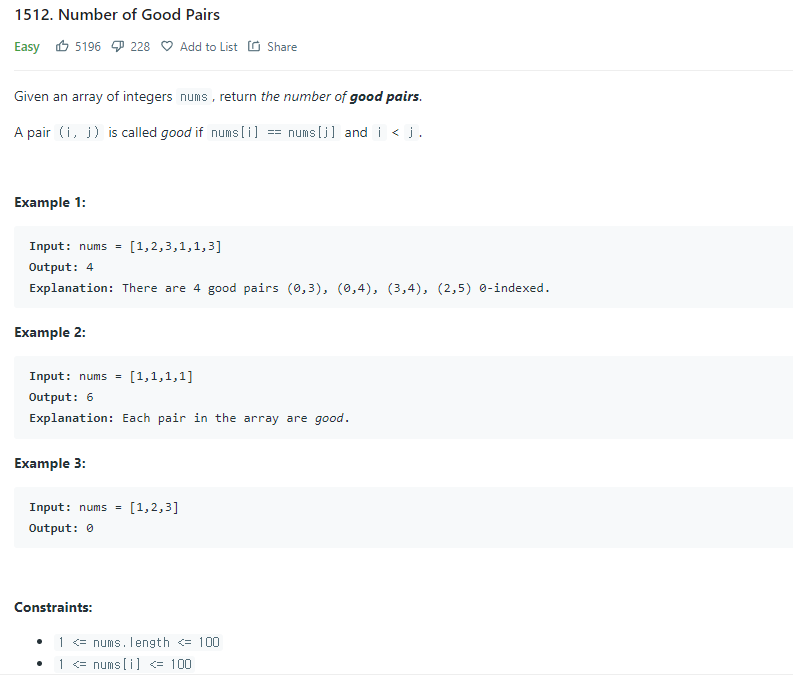
https://leetcode.com/problems/number-of-good-pairs/
1. 접근
1.TwoSum 문제와 유사하게 확인한 요소를 딕셔너리에 저장하는 것을 활용해볼 수 있겠다고 생각했다.
추가적으로, i < j라는 조건 상, i와 j의 순서가 바뀔 수 없으므로 (j, i)의 형태의 쌍은 나오지 않을 것이라 생각했다. 그래서 이미 딕셔너리에 값이 저장된 경우면, 딕셔너리에 저장되어 있는 값의 수 만큼 경우를 추가해주도록 하면 될 것으로 보였다.
2. 제출한 답
1
2
3
4
5
6
7
8
9
10
11
12
from collections import defaultdict
class Solution:
def numIdenticalPairs(self, nums: List[int]) -> int:
seen = defaultdict(int)
answer = 0
for num in nums:
if num in seen:
answer += seen[num]
seen[num] += 1
return answer
키를 처음 딕셔너리에 넣을 때, 0을 기본적인 값으로 세팅하도록 디폴트값이 int인 딕셔너리 생성.
받은 소스 숫자들을 반복해서 돌면서 O(n)만약 딕셔너리 안에 해당 값이 있으면 O(1)
answer에 딕셔너리에 있는 값만큼 케이스가 더 있으므로, 해당 값을 결과값에 더해준다
아니면 딕셔너리의 값에 1을 더해준다(기본값 0)
의 구조다.
시간복잡도
시간 복잡도는 O(n)이다.
3. in에 대해
이걸 풀고 시간복잡도에 대해 알아보면서 파이썬의 in 연산자에 대해 조금 더 알게 됐다. 나는 in이 객체의 내용물을 모두 순회하는 개념인 줄 알았다. 하지만 그보다는 ‘존재 여부를 조회’ 한다는 것에 가까운 개념인 것 같다.
리스트, 튜플, 문자열과 같은 시퀀스에서는 O(n)의 시간복잡도를 가진다. 하지만 딕셔너리나 세트와 같은 경우에는 시간복잡도가 O(1)이다.
세트는 왜 시간복잡도가 O(1)이지?
세트가 내부적으로 해시 테이블을 사용하기 때문이다. 원하는 요소에 직접 접근이 가능하기 때문에 모든 요소를 순회하면서 다 확인할 필요가 없다. (해시 충돌-두 개 이상의 입력 값에 대해 해시 함수가 동일한 해시 값을 생성하는 상황 - 이 많이 발생하는 최악의 경우에는 시간 복잡도가 O(n)이 될 수 있지만 이는 일반적이지 않다고 한다.)
그래서, 리스트와 달리 요소의 수에 비례해 시간이 증가하지 않기 때문에 포함 여부를 자주 확인해야하는 많은 요소를 다룰 때는 세트를 사용하는 것이 좋다.
4. 추가공부
더 나은 풀이 방법
해시 충돌